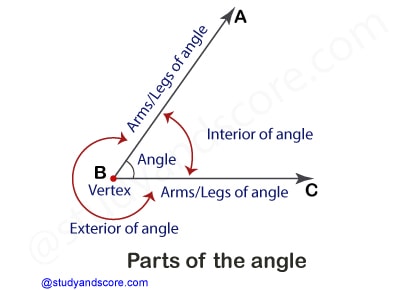
Bisector of an angle is a ray which divides the interior of the angle into two equal measures. In other words, it is a line which cuts an angle into two equal angles. Bisector of an angle is also known as angle bisector. Angle bisector passes through the vertex of the angle. An angle bisector can be external or internal.
Internal angle bisector: In the given figure below, the ray OX bisects the internal angle ∠XYZ. Now ∠XYO and ∠OYZ are congruent.
Therefore ∠XYO ≅ ∠OYZ
Here OX is the internal angle bisector.
Exterior angle bisector: In the given figure below, the ray OM bisects the external angle ∠X1YZ. Now ∠ X1YO and ∠OYZ are congruent.
Therefore ∠X1YO ≅ ∠OYZ.
Here OM is the external angle bisector.
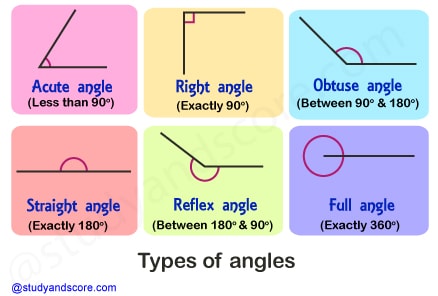
The following is the detailed study of few important types of angles which are useful in geometry.
For example let us consider two parallel lines X1 and X2. Now let another line AB intersect both the parallel lines X1 and X2. The following are the facts that can be observed from these lines.
Corresponding angles are equal
∠1=∠5
∠4=∠8
∠2=∠6
∠3=∠7
Alternate interior angles are equal
∠3=∠5
∠4=∠6
Vertically opposite angles are equal
∠2=∠4
∠1=∠3
∠5=∠7
∠6=∠8
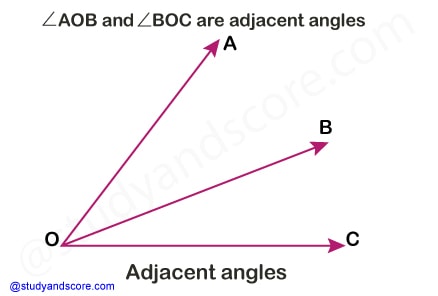
Two angles are called as adjacent angles, when they have a common side and common vertex. Their interiors are separate and these angles do not overlap. In the given example figure, ∠AOB and ∠BOC are adjacent angles.
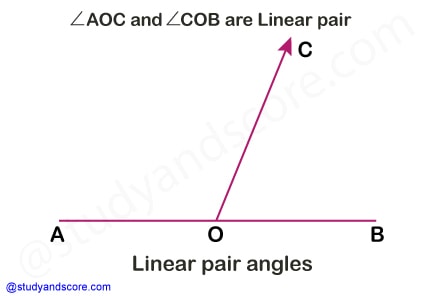
Two angles are called a linear pair, when they have a common side and their other two sides are opposite rays. The angles that form a linear pair are always adjacent. The sum of angles in a linear pair is 180°. In the given example figure, ∠AOC and ∠COB form a linear pair. Because ∠AOC + ∠COB= 180°
If the sum of two angles is 90°, then they are called complimentary angles. Each angle is complement of the other angle. If ∠AOC + ∠COB= 90°, then ∠AOC and ∠COB are complementary angles.
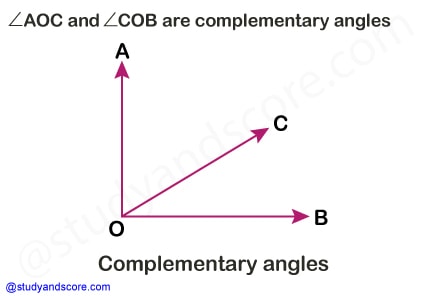
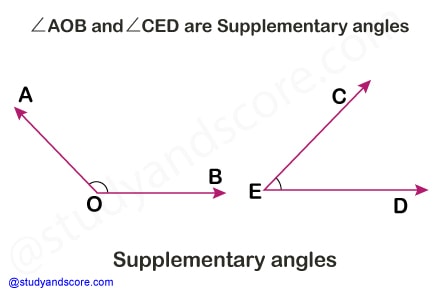
If the sum of two angles is 180°, then they are called supplementary angles. Each angle is supplement of the other angle. The angles of linear pair are supplementary angles.
∠AOB + ∠CED= 120° + 60° = 180°
Therefore these angles are supplementary
Two angles are said to be vertically opposite angles if their sides form two pairs of opposite rays. In other words, when two lines intersect, two pairs of vertically opposite angles are formed. These are the angles opposite to each other when two lines cross each other. For example, let us consider two lines AB and DC intersecting at point ‘O’.
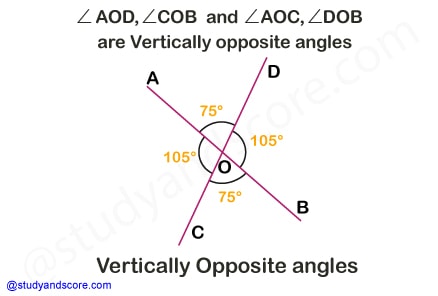
From this we can deduce the following,
Vertically opposite angles are similar or congruent in nature,
∠AOC and ∠DOB are vertically opposite (∠AOC ≅ ∠DOB)
∠AOD and ∠COB are also vertically opposite (∠AOD ≅ ∠COB)
Sum of all angles at the intersection point is 360°, ∠AOC+∠DOB+∠AOD+∠COB= 360°
When two lines are intersected by a transversal, then they form four pairs of corresponding angles. For example, let us consider two lines EF and GH being intersected at points B and C by the transversal line AD.
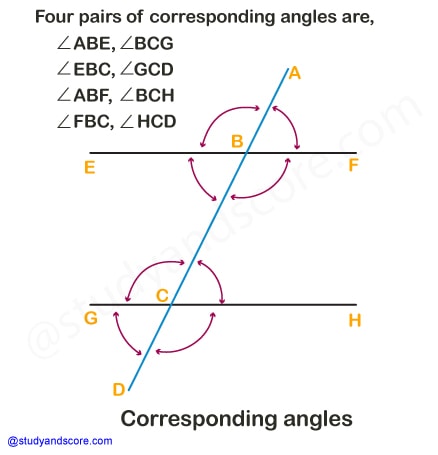
From this we can deduce the following,
The four pairs of corresponding angles are,
∠ABE, ∠BCG
∠EBC, ∠GCD
∠ABF, ∠BCH
∠FBC, ∠HCD
When two parallel lines are intersected by a transversal line, the pair of corresponding angles so formed is congruent.
Hence is EF is parallel to GH and AD is the transversal line then,
∠ABE ≅ ∠BCG
∠EBC ≅ ∠GCD
∠ABF ≅ ∠BCH
∠FBC ≅ ∠HCD
Conversely, if the transversal line intersects two lines and if one pair of corresponding angles is congruent then two lines are parallel. Hence, when one pair of corresponding angles is congruent, then all the pairs of corresponding angles are congruent.
When two parallel lines are intersected by a transversal line, they form two pairs of alternate angles.
∠EBC, ∠BCH
∠FBC, ∠GCB
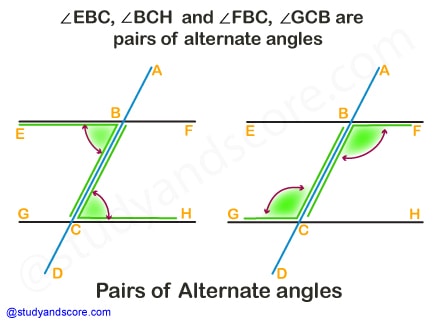
When two parallel lines are intersected by a transversal line, the pairs of alternate angles so formed are congruent.
∠EBC ≅ ∠BCH
∠FBC ≅ ∠GCB
Conversely, if the transversal line intersects two lines and if one pair of alternate angles is congruent then two lines are parallel. Hence, when one pair of alternate angles is congruent, then all the pairs of alternate angles are congruent.
When two lines are intersected by a transversal line, they form two pairs of interior angles. For example, the two pairs of interior angles in the given figure are ∠EBC, ∠GCB and ∠FBC, ∠BCH
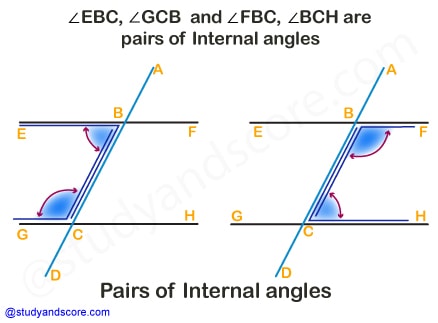
When two parallel lines are intersected by a transversal line, the pairs of interior angles so formed are supplementary.
∠EBC+∠GCB=180°
∠FBC+∠BCH=180°
Conversely, if the transversal line intersects two lines and if one pair of interior angles is supplementary then two lines are parallel. Hence, when one pair of interior angles is supplementary, the other pair is also supplementary. And all the pairs of alternate and corresponding angles are congruent.
- Share with your friends! -
Login to post your comment here...
- or with social Account -