Basic Geometry: Types of Angles
Posted on : 12-07-2018 Posted by : Admin

Introduction

• Angle is the shape formed by the union of two rays diverting from a common endpoint.
• This common endpoint from which the two lines divert is called as vertex.
• The two straight sides of the angle are called its legs or arms.
• The area between the rays that make up an angle is known as interior of the angle. Interior of the angle extends away from the vertex to infinity.
• The remaining place on the plane which does not belong to interior is called as exterior of the angle.     
• Two angles are said to be congruent if their measurements are equal. It is denoted by ≅.

 

Bisector of an angle

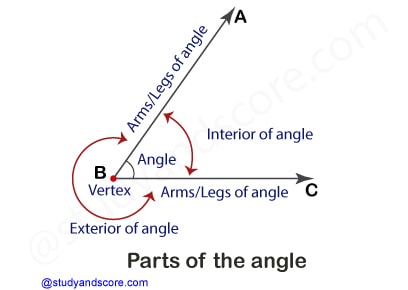
Bisector of an angle is a ray which divides the interior of the angle into two equal measures. In other words, it is a line which cuts an angle into two equal angles.  Bisector of an angle is also known as angle bisector. Angle bisector passes through the vertex of the angle. An angle bisector can be external or internal.

Internal angle bisector: In the given figure below, the ray OX bisects the internal angle ∠XYZ. Now ∠XYO and ∠OYZ are congruent.

Therefore ∠XYO ≅ ∠OYZ

Here OX is the internal angle bisector.

Exterior angle bisector: In the given figure below, the ray OM bisects the external angle ∠X1YZ. Now ∠ X1YO and ∠OYZ are congruent.

Therefore ∠X1YO ≅ ∠OYZ.

Here OM is the external angle bisector.

 

Types of angles

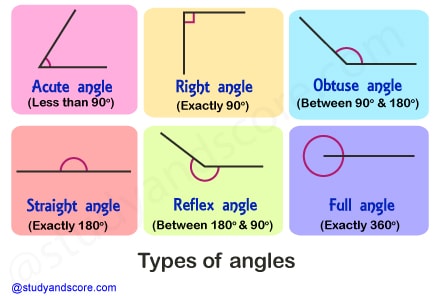
The following is the detailed study of few important types of angles which are useful in geometry.

1. Acute angle: The angle whose value lies between 0 to 90° is called acute angle.
2. Right angle: The angle whose value is 90° is called right angle.
3. Obtuse angle: The angle whose value lies between 90 to 180° is called obtuse angle.
4. Straight angle: The angle whose value is 180° is called straight angle.
5. Reflex angle: The angle whose value lies between 180 to 360° is called reflex angle.
6. Full angle: The angle whose value is 360° is called complete or full angle.  This angle is also known as full rotation angle.

---

---

 

Pairs of angles

 

Adjacent angles

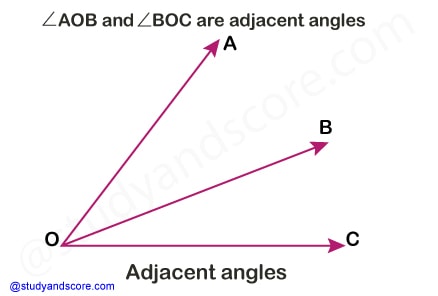
Two angles are called as adjacent angles, when they have a common side and common vertex. Their interiors are separate and these angles do not overlap. In the given example figure, ∠AOB and ∠BOC are adjacent angles.

 

Linear pair

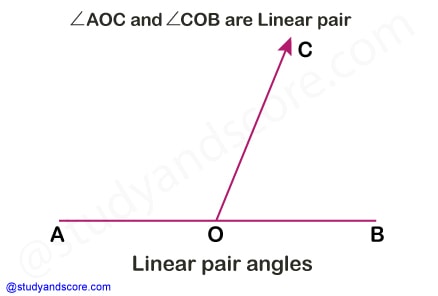
Two angles are called a linear pair, when they have a common side and their other two sides are opposite rays. The angles that form a linear pair are always adjacent. The sum of angles in a linear pair is 180°. In the given example figure, ∠AOC and ∠COB form a linear pair. Because ∠AOC + ∠COB= 180°

 

Complimentary angle

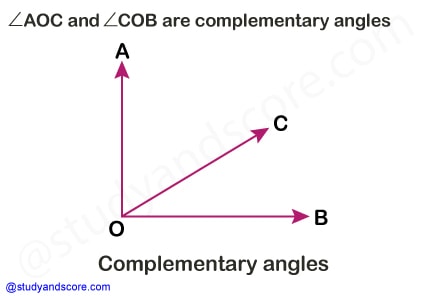
If the sum of two angles is 90°, then they are called complimentary angles. Each angle is complement of the other angle.  If ∠AOC + ∠COB= 90°, then ∠AOC and ∠COB are complementary angles.

 

Supplementary angle

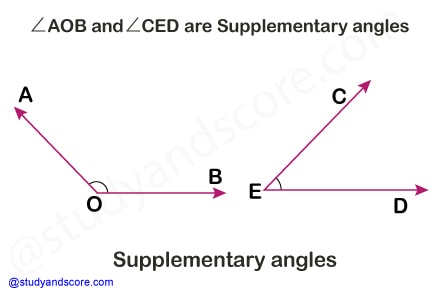
If the sum of two angles is 180°, then they are called supplementary angles. Each angle is supplement of the other angle. The angles of linear pair are supplementary angles.

∠AOB + ∠CED= 120° + 60° = 180°

Therefore these angles are supplementary

 

Vertically opposite angles

Two angles are said to be vertically opposite angles if their sides form two pairs of opposite rays. In other words, when two lines intersect, two pairs of vertically opposite angles are formed. These are the angles opposite to each other when two lines cross each other. For example, let us consider two lines AB and DC intersecting at point ‘O’.

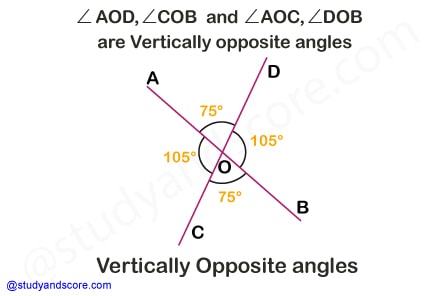
From this we can deduce the following,

Vertically opposite angles are similar or congruent in nature,

∠AOC and ∠DOB are vertically opposite (∠AOC ≅ ∠DOB)

∠AOD and ∠COB are also vertically opposite (∠AOD ≅ ∠COB)

Sum of all angles at the intersection point is 360°, ∠AOC+∠DOB+∠AOD+∠COB= 360°

 

Corresponding angles

When two lines are intersected by a transversal, then they form four pairs of corresponding angles. For example, let us consider two lines EF and GH being intersected at points B and C by the transversal line AD.

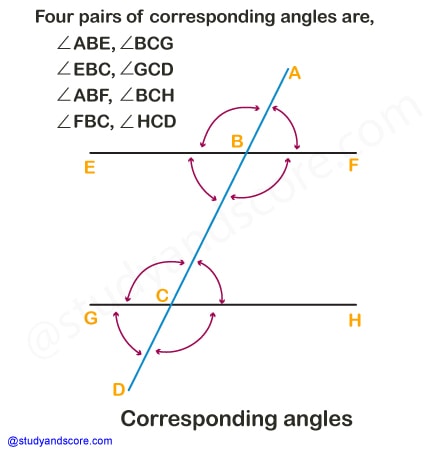
From this we can deduce the following,

The four pairs of corresponding angles are,

∠ABE, ∠BCG

∠EBC, ∠GCD

∠ABF, ∠BCH

∠FBC, ∠HCD

When two parallel lines are intersected by a transversal line, the pair of corresponding angles so formed is congruent.

Hence is EF is parallel to GH and AD is the transversal line then,

∠ABE ≅ ∠BCG

∠EBC ≅ ∠GCD

∠ABF ≅ ∠BCH

∠FBC ≅ ∠HCD

Conversely, if the transversal line intersects two lines and if one pair of corresponding angles is congruent then two lines are parallel. Hence, when one pair of corresponding angles is congruent, then all the pairs of corresponding angles are congruent.

 

Alternate angles

When two parallel lines are intersected by a transversal line, they form two pairs of alternate angles.

∠EBC, ∠BCH

∠FBC, ∠GCB

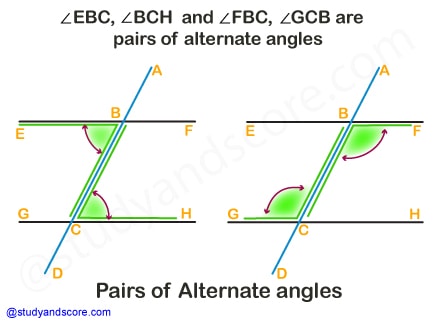
When two parallel lines are intersected by a transversal line, the pairs of alternate angles so formed are congruent.

∠EBC ≅ ∠BCH

∠FBC ≅ ∠GCB

Conversely, if the transversal line intersects two lines and if one pair of alternate angles is congruent then two lines are parallel. Hence, when one pair of alternate angles is congruent, then all the pairs of alternate angles are congruent.

 

Interior angles

When two lines are intersected by a transversal line, they form two pairs of interior angles. For example, the two pairs of interior angles in the given figure are ∠EBC, ∠GCB and ∠FBC, ∠BCH

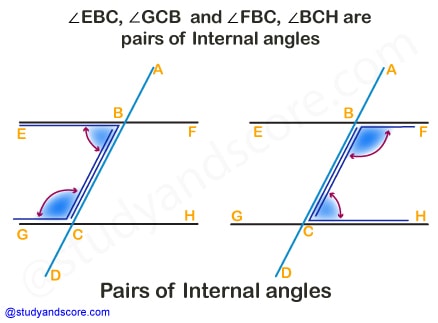
When two parallel lines are intersected by a transversal line, the pairs of interior angles so formed are supplementary.

∠EBC+∠GCB=180°

∠FBC+∠BCH=180°

Conversely, if the transversal line intersects two lines and if one pair of interior angles is supplementary then two lines are parallel. Hence, when one pair of interior angles is supplementary, the other pair is also supplementary. And all the pairs of alternate and corresponding angles are congruent.

---