
Analytical reasoning involves questions where the candidates need to count the number of geometrical shapes present in the given complex question figure. These types of questions require a systematic approach. First of all candidate must analyze the given complex question figure and then go on to determine the number of shapes in question.
These types of questions are very important in competitive exams like GRE, Bank exams, Civil services, IBPS PO and Clerk. So let us study well and score more on this topic.
A few examples of the types of questions asked in the exam are given below,
There are many types of embedded figure questions. A few of them are explained below,
Consider the following example,
In each of the following question, find the minimum number of straight lines required to make the given figure.
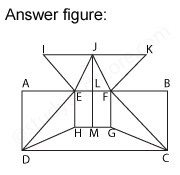
After labelling the figure, we get the following,
Total number of straight lines in the figure are 4+5+8=17
Consider the following example,
In each of the following question, find the minimum number of triangles in the given figure.
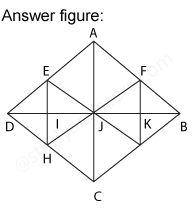
After labelling the figure, we get the following,
Total number of triangles in the figure is 12 + 8 + 4 + 4 = 28
Consider the following example,
In each of the following questions, count the number of squares in the figure.
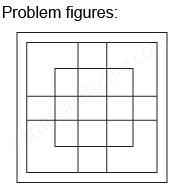
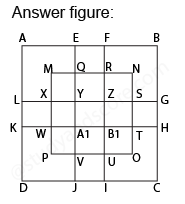
After labelling the figure, we get the following,
Total number of squares in the figure is 13 + 4 + 4 + 4 + 1 + 1 = 27
Consider the following example,
In each of the following question, count the number of parallelogram in the given figure.
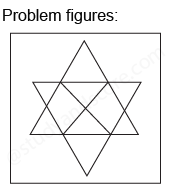
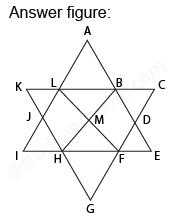
After labelling the figure, we get the following,
Total number of parallelograms in the figure is 2 + 2 + 8 + 3 = 15
How many rectangles are there in the following figure.
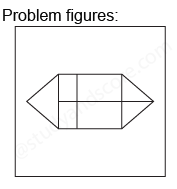
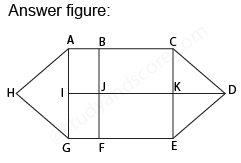
After labelling the figure, we get the following,
Total number of Rectangles in the figure is 4 + 4 + 1 = 9
In each of the the following question, count the number of triangles and squares in the given figure.
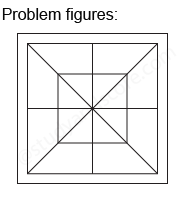
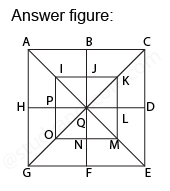
After labelling the figure, we get the following, Simplest triangles IJQ, JKQ, KLQ, LMQ, MNQ, NOQ, OPQ, and PIQ (8)
Total number of triangles in the figure is 8 + 12 + 8 + 4 = 32
Also we need to count the number of squares in this figure,
Total number of squares in the figure is 4 + 4 + 1 + 1 = 10
Hence option C is correct.

Hope you have liked this post.
Please share it with your friends through below links.
All the very best from Team Studyandscore
“Study well, Score more…”
- Share with your friends! -
Login to post your comment here...
- or with social Account -