
A series is an ordered collection of figures or numbers or words or alphabets. A sequence of numbers which follow a particular pattern is called number series. In number series questions, some specific pre-decided rules are hidden and the candidate needs to find at that hidden rule to arrive at correct answer.
For example, consider 1, 4, 7, 10, 13….. Here the difference between the consecutive numbers is three. It is important to note that in number series each number except the first number is related to the prior number with some specific rule.
There are many types of number series. A few of them are explained below,
Arithmetic Series: In this type the series progresses with addition or subtraction of some specific numbers. Here the DIFFERENCE between any successive terms is not very large, increases in a specific manner and is constant throughout the series.
Example: 5, 10, 17, 26, 37, 50, 65
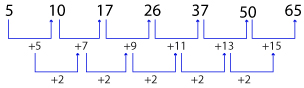
Geometric Series: In this type the series progresses with addition or subtraction of some specific numbers. Here the RATIO between any successive terms is large, increases in a specific manner and is constant throughout the series.
Example: 4, 12, 36, 108, 324, 972

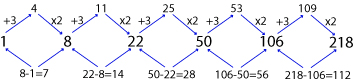
Arithmetico-Geometric Series: As name suggests this series is the combination of arithmetic and geometric series. An important property of such series is that the DIFFERENCE of successive terms is in geometric series.
Example: 1, 8, 22, 50, 106, 218
Product series: In this type of series, each term is multiplied by a fixed number or specific number pattern to get the next successive number. This can be of following types,
Example: 2, 4, 8, 16, 32, 64, 128

Example: 30, 180, 900, 3600, 10800, 21600

Example: 21, 105, 630, 4410, 35280

Difference Series: Difference series can be further classified as
Example: 3, 6, 9, 12, 15, 18, 21

Example: 1, 2, 4, 7, 11, 16, 22

Here the difference is increasing from left to right
Example: 7, 16, 24, 31, 37, 42

Here the difference is decreasing from left to right
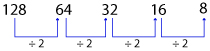
Division series: In this type of series, each term is divided by a fixed number or specific number pattern to get the next successive number.
Example: 128, 64, 32, 16, 8
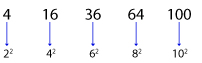
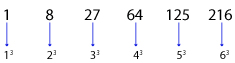
Square or cube series: This type of numbers series progresses with squaring or cubing of the numbers.
Example: 4, 16, 36, 64, 100 (squaring)
Example: 1, 8, 64, 125, 216, 343 (Cubing)
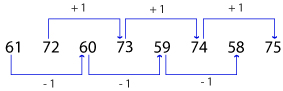
Mixed series: In this type, more than one series pattern is involved. Generally these type of questions are a little complicated.
Example: 61, 72, 60, 73, 59, 74, 58, 75

Number series questions are common in any competitive exam. Candidates can score good marks with just the basic knowledge of math. These questions are relatively easy provided the candidate is able to find out the hidden rule. Here Studyandscore provides you with basic tips and tricks to solve number series questions. After you read through this article, click below to revise and practice with our tests.
Let us see the types of number series questions and tricks to solve them
In these questions, the candidate must find the missing term in the given number series.
For example: Find the number which must come in place of question mark in the below given series
17, 19, 25, 37, ?, 87
The given series follows the below pattern,
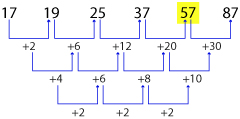
So, 57 comes in place of (?)
In these questions, one of the number does not follow the specific rule being followed by all other numbers of the series. Candidates need to spot this odd number.
For example: Find the odd term in the following given series
13, 16, 21, 27, 39, 52, 69
The given number series follows the below pattern,
So, 27 is the odd term in the given series
In these questions, one of the number does not follow the specific rule being followed by all other numbers of the series. Candidates need to spot this odd number and replace it with the correct number from the given options.
For example: Find out the odd term from the following number series and replace it with the correct term.
484, 240, 120, 57, 26.5, 11.25, 3.625
The given number series follows the below pattern,
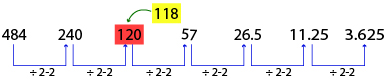
So, 120 is the odd term in the given series and it must be replaced by 118
In these questions, first the value of the missing term is to be found. Then, using this value find the value of unknown variable in the given expression. These kind of questions are relatively a bit complicated.
For example: Find the value of 'n' in the given series and using this value of 'n', find the value of x in the given expression..
68, 68.5, 69.5, 71, n, 75.5, 78.5. Replace the value of 'n' in expression n×121+x=10000
The given number series follows the below pattern,
68+0.5= 68.5
68.5+1= 69.5
69.5+1.5= 71
71+2= 73
73+2.5= 75.5
75.5+3= 78.5
So n= 73
Replacing the value of 'n' in the given expression,
n×121+x=10000
⇒ 73×121+x=10000
⇒ 8833+x=10000
⇒ x=10000-8833=1167
In these questions, two series patterns are given. The pattern of the second series is same as the first series. Based on the first series, candidate needs to find out the unknown term in second series.
For example: In series-1, only one number is wrong. If the wrong number is corrected, the series gets established following a certain logic. Complete series-2 with same logic and find what will come in place of (c)?
| Series 1 | 5 | 9 | 25 | 91 | 414 | 2282.5 |
|---|---|---|---|---|---|---|
| Series 2 | 3 | a | b | c | d | e |
⇒ 5×1.5+1.5= 7.5+1.5= 9
⇒ 9×2.5+2.5= 22.5+2.5= 25
⇒ 25×3.5+3.5= 87.5+3.5= 91
⇒ 91×4.5+4.5= 409.5+4.5= 414
⇒ 414×5.5+5.5= 2277+5.5= 2282.5
Similarly, series 2
(a)⇒ 3×1.5+1.5= 4.5+1.5= 6
(b)⇒ 6×2.5+2.5= 15+2.5= 17.5
(c)⇒ 17.5×3.5+3.5= 6125+3.5= 64.75
| BASED ON DIFFERENCE BETWEEN TWO CONSECUTIVE TERMS OF A SERIES |
|
Difference between two consecutive terms is same For example: |
|
Difference between two consecutive terms is in arithmetic progression (AP) For example: *Here 11, 16, 21 are in AP in example 1 whereas -9, -7, -5 are in AP example 2. |
|
Difference between two consecutive terms is a perfect square For example: |
|
Difference between two consecutive terms are multiples of a number For example: *Here 12, 24, 48 are multiples of 12 in example 1 whereas -44, -33, -22 are multiples of 11 example 2. |
|
Difference between two consecutive terms is a perfect Cube For example: |
|
Difference between two consecutive terms is in geometric progression (GP) For example: *Here 1, 3, 9, 27 are in GP in example 1 whereas -16, -8, -4, -2 are in GP example 2. |
| BASED ON RATION BETWEEN TWO CONSECUTIVE TERMS OF A SERIES |
|
Ratio between two consecutive terms is same For example: |
|
Ratio between two consecutive terms is a Prime number For example: *Here 2, 3, 5 are prime numbers in example 1 whereas 11, 7, 5 are prime numbers example 2. |
|
Ratio between two consecutive terms is in arithmetic progression (AP) For example: *Here 2, 4, 6 are in AP in example 1 whereas 5, 4, 3 are in AP example 2. |
|
Ratio between two consecutive terms is a perfect square For example: |
|
Ratio between two consecutive terms are multiples of a number For example: *Here 2, 4, 8 are multiples of 2 in example 1 whereas 9, 6, 3 are multiples of 3 example 2. |
|
Ratio between two consecutive terms is a perfect Cube For example: |
|
Ratio between two consecutive terms is in geometric progression (GP) For example: *Here 1, 3, 9, 27 are in GP in example 1 where a -16, -8, -4, -2 are in GP example 2. |
Hope you have liked this post.
Please share it with your friends through below links.
All the very best from Team Studyandscore
“Study well, Score more…”
- Share with your friends! -
Login to post your comment here...
- or with social Account -