Pipes and Cisterns: Basic Concept, Formulae and Short tricks
Posted on : 03-08-2018 Posted by : Admin

Pipes, Cisterns, Basic Concept, Formula, Short tricks, pipes examples, cisterns examples, pipes and cistern problems with solutions

Introduction

The questions on pipes and cisterns are asked in every competitive exam. In general the questions of pipes and cisterns can be solved by using the methods of work and time. In competitive examinations, these questions are asked in the form of word problems with the concept similar to work and time.

The basic structure of these types of questions is,

A tank has to be filled or emptied by two or more pipes
Time taken by each pipe to fill or empty the tank is given or should be found
Total time taken to fill or empty the tank is given or should be found

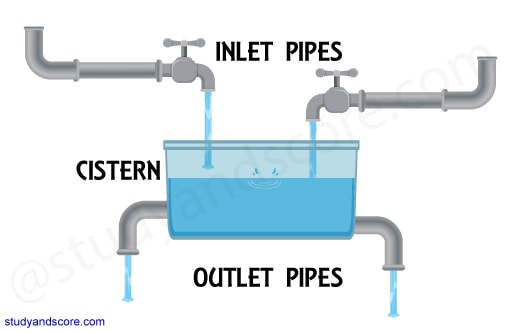
Pipes: Pipes are tubes which are connected to tanks to fill in or empty out some liquid. Tanks are also called as Cisterns or reservoirs. So basically these questions are related to the efficiency of pipes to fill or empty the tanks.

The pipes can be of two types namely,

Inlet pipe: As the name suggests these pipes are used to fill or send the liquid into the tank. In other words, Inlet pipes fill the tanks.

Outlet pipe: As the name suggests these pipes are used to empty or send the liquid out of the tank. In other words, outlet pipes empty the tanks. It may also be mentioned as Leak.

Pipes, Cisterns, Basic Concept, Formula, Short tricks, pipes examples, cisterns examples, pipes and cistern problems with solutions

Formulae and short tricks

The following are few formulae and short tricks for solving questions relating to Pipes and cisterns:

Formula 1:

If pipe A can completely fill a tank in x hours, then the portion filled in 1 hour is $\frac{1}{x}$ . (or) If pipe A fills $\frac{1}{x}$ portion of the tank in 1 hour, then the time taken by the pipe to fill the full tank is x hours.

Example: If a pipe fully fills a tank in 10 hours, what part of the tank will be filled by the pipe in 1 hour?

Solution: According to the above given formula, if pipe can comletely fill a tank in x hours, then the portion filled in 1 hour is $\frac{1}{x}$

Hence, $\frac{1}{10}$ ^thpart of the tank will be filled by the pipe in 1 hour.

Formula 2:

If pipe A can completely empty a tank in y hours, then the portion emptied in 1 hour is $\frac{1}{y}$ (or) If pipe A empties $\frac{1}{y}$ portion of the tank in 1 hour, then the time taken by the pipe to empty the full tank is y hours.

Example: If an outlet pipe can empty a cistern in 15 hours, in what what time can the pipe empty 3/5 of the cistern?

Solution: According to the above given formula, if pipe can comletely empty a tank in y hours, then the portion emptied in 1 hour is $\frac{1}{y}$

so, $\frac{3}{5} \times 15 = 9 hours$

Hence, $\frac{3}{5}$ ^th part of the tank will be emptied by the pipe in 9 hours.

Formula 3:

If pipe A fills a tank in x hours and another pipe B fills a tank in y hours, then the time taken by both pipes together to fill the tank is $\frac{xy}{x + y}$ hours.

Example: If a pipe can fill a tank in 2 hours and another pipe can fill the same tank in 8 hours, then what part of the tank can be filled by both the pipes when opened simultaneously?

Solution: According to the above given formula, if pipe A can comletely fill a tank in x hours and pipe B can comletely fill a tank in y hours, then the time taken by both pipes together to fill the tank is $\frac{xy}{x + y}$ hours.

So, $\frac{2 \times 8}{2 + 8} = \frac{16}{10} = \frac{8}{5} part$

Hence, $\frac{8}{5}$ ^th part of the tank will be filled by both the pipe when opened simultaneously.

Click to practice More questions on this topic...

Formula 4:

If pipe A fills a tank in x hours and another pipe B empties the tank in y hours (where y>x), then the time taken to fill the tank when both the pipes are open is $\frac{xy}{y - x}$ hours.

Example: If a pipe can fill a tank in 5 hours and another pipe can empty the same tank in 7 hours. If both the pipes are opened simultaneously, how much time will be taken to fill the tank?

Solution: According to the above given formula, if pipe A can comletely fill a tank in x hours and pipe B can empty the same tank in y hours, then the time taken to fill the tank when both the pipes are opened simultaneously is $\frac{xy}{y - x}$ hours.

so, $\frac{5 \times 7}{7 - 5} = \frac{35}{2} = 17.5 hours$

Hence, the tank will be filled in 17.5 hours when both the pipes are opened simultaneously.

Formula 5:

If pipe A fills a tank in x hours and another pipe B empties the tank in y hours (where x>y), then the time taken to fill the tank when both the pipes are open is $\frac{xy}{x - y}$ hours.

Example: If a pipe can fill a tank in 15 hours and another pipe can empty the same tank in 8 hours. If both the pipes are opened simultaneously, how much time will be taken to fill the tank?

So, $\frac{15 \times 8}{15 - 8} = \frac{120}{7} = 17.14 hours$

Hence, the tank will be filled in 17.14 hours when both the pipes are opened simultaneously.

Formula 6:

If three pipes A, B and C can fill the tank separately in x hours, y hours and z hours respectively then, the time taken by all the three pipes together to fill the tank is $\frac{xyz}{xy + yz + zx}$ hours.

Example: Three pipes x, y, z fill a tank in 4, 5, and 6 hours respectively. The time taken by all the three pipes to fill the tank when opened simultaneously is?

Solution: According to the above given formula, If three pipes A, B and C can fill the tank separately in x hours, y hours and z hours respectively then, the time taken by all the three pipes together to fill the tank is $\frac{xyz}{xy + yz + zx}$ hours.

So,

$\frac{4 \times 5 \times 6}{(4 \times 5) + (5 \times 10) + (10 \times 4)} = \frac{200}{110} = \frac{20}{11} or 1 \frac{9}{11} hours$

Hence, the tank will be filled in $1 \frac{9}{11}$ hours when all the pipes are opened simultaneously.

Click to practice More questions on this topic...

Formula 7:

If pipe A and B fills a tank in x and y hours respectively, but a third pipe C empties the full tank in z hours then the net portion filled in 1 hour when all of them are opened together is $\frac{xyz}{yz + xz - xy}$ hours.

Example: Two pipes x, y fill a tank in 20, 10 hours respectively. The third pipe z empties the full tank in 30 hours. If all the three are opened simultaneously, how much time will be required to fill the tank?

Solution: According to the above given formula, If pipe A and B fills a tank in x and y hours respectively, but a third pipe C empties the full tank in z hours then the net portion filled in 1 hour when all of them are opened together is $\frac{xyz}{yz + xz - xy}$ hours.

So,

$\frac{20 \times 10 \times 30}{(10 \times 30) + (20 \times 30) - (20 \times 10)} = \frac{6000}{700} = \frac{60}{7} or 8 \frac{4}{7} hours$

Hence, the tank will be filled in $8 \frac{4}{7}$ hours when all the pipes are opened simultaneously.

Formula 8:

Two pipes A and B can fill the tank in x and y min respectively. If both pipes are opened together, then the time after which pipe B should be closed so that the tank is full in t min is $\{y [1 - \frac{t}{x}]\}$ min.

Example: Two pipes m and n can fill a tank in 12, 6 min respectively. If both the pipes are opened simultaneously, after how much time should pipe n be closed so that the tank is full in 4 min?

Solution: According to the above given formula, If Two pipes A and B can fill the tank in x and y min respectively. If both pipes are opened together, then the time after which pipe B should be closed so that the tank is full in t min is $\{y [1 - \frac{t}{x}]\}$ min.

So, $\{6 [1 - \frac{4}{12}]\} = 6 \times \frac{8}{12} = 4 \min$

Hence, the tank will be filled in 4 min both the pipes are opened simultaneously.

Formula 9:

Two pipes A and B can together fill a tank in time T. If time taken by pipe A alone is more than T by x and the time taken by pipe B alone is more than T by y, then T is $\sqrt{xy}$ min.

Example: Two pipes 'a' and 'b' together can fill the tank. Both the pipes fill the tank in time 'T'. If 'a' alone takes 44 min more time than 'T' to fill the tank completely and 'b' alonge takes 20 min more time than 'T' to fill the tank completely, find the value ot 'T'.

Solution:According to the above given formula, Two pipes A and B can together fill a tank in time T. If time taken by pipe A alone is more than T by x and the time taken by pipe B alone is more than T by y, then T is $\sqrt{xy}$ min.

So, $T = \sqrt{44 \times 20} = \sqrt{64} = 8 \min$

Hence, the tank will be completely filled in 8 min.

Formula 10:

Suppose we have many pipes, where some fill the tank and some empty the tank. If we open all of them together, then in one hour,

the part of the tank filled is ∑ (1 / x_i) + ∑ (1 / y_o)

the part of the tank emptied is ∑ (1 / x_i) - ∑ (1 / y_o)

where ‘x_i‘ is the time taken by inlet pipe ‘i’ to fill the tank completely if only it was open and ‘y_o‘ is the time taken by outlet pipe ‘o’ to empty the tank completely if only it was open.

Click to practice More questions on this topic...

Hope you have liked this post.

Please share it with your friends through below links.

All the very best from Team Studyandscore

“Study well, Score more…”

- Share with your friends! -

Pipes and Cisterns: Basic Concept, Formulae and Short tricks Posted on : 03-08-2018 Posted by : Admin

Introduction

Formulae and short tricks

Login to post your comment here...

- or with social Account -

Pipes and Cisterns: Basic Concept, Formulae and Short tricks
Posted on : 03-08-2018 Posted by : Admin